IDES (Integrated Discrete-Event Systems) [1] is a tool that allows us to create state diagrams and perform some discrete system operations, like closure, parallel composition, reachable, trim, etc. With the aid of IDESParser tool, we can export an IDES model into a Markov chain and perform transient and steady-state analysis on the SHARPE[2] or Mathematica [3] packages.

Here is the basic usage of the package:

java -jar IDESParser.jar <file name.xmd> --mathematica

or:

java -jar IDESParser.jar <file name.xmd> --mathematica9

or:

java -jar IDESParser.jar <file name.xmd> --linearsystem

or:

java -jar IDESParser.jar <file name.xmd> --sharpe <sharpe project name> <sharpe model name>

We invoke the program with the “java – -jar IDESParser.jar” command (requires version 7 of JRE), followed by the name of the IDES model and the output format argument. We have four possible formats of output:

• As Mathematica input for the “StateDiagrams.m” [4] package (with – -mathematica argument)
• As Mathematica source code for the new functions of Mathematica 9 (with – -mathematica9 argument)
• As a linear system of balance state equations, represented as Mathematica code (with – -linearsystem argument)
• As a SHARPE Markov chain model (with – -sharpe argument)

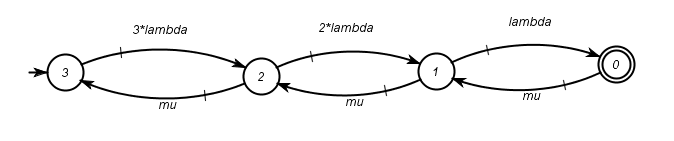
In the Figure 1 we have a state diagram created on IDES that represents a birth-death Markov Chain for evaluating availability of a system composed by three components in parallel. The fault mode of the system is when we don’t have any running component, represented by state .

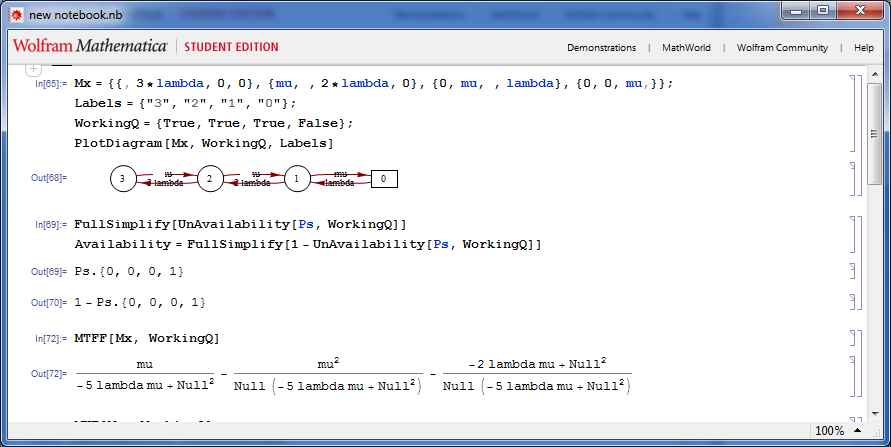
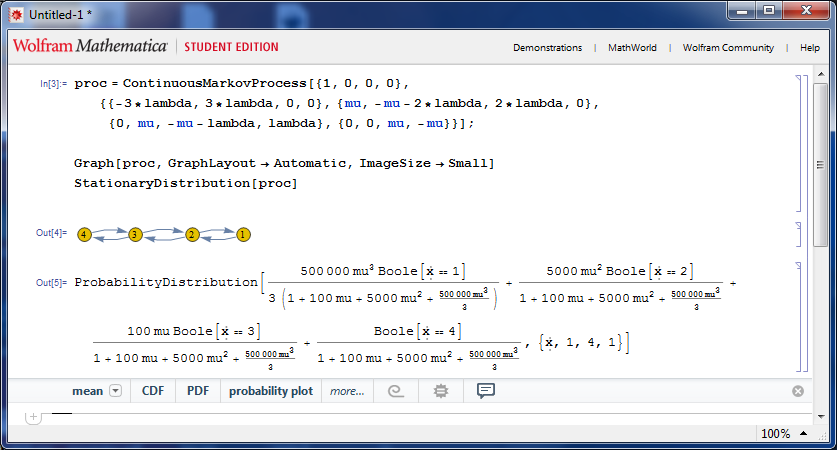
For obtaining closed formulas for steady state probabilities, system availability, etc., we can use the – -mathematica command line argument and generate code compatible with the StateDiagrams.m package for Mathematica. The code generated by IDESParser and the resulting output is shown on the Figure 2. If we want to use the new functions provided by Mathematica 9, we add the – -mathematica9 command line argument. The generated code and resulting output is displayed on Figure 3.

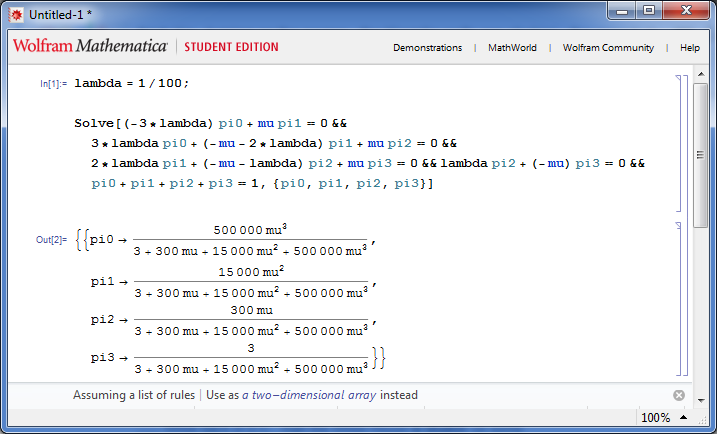
In some situations, the markov chain has to many states and transitions, and consequently we can’t obtain closed formulas for steady state probability. We have two ways to deal with this problem. The first way is to fix some parameters, and obtaining closed equations for the other parameters left open. We can generate the linear system with the – -linearsystem argument, and set the parameters we want to fix. Figure 4 shows the code generated by IDESParser and the output generated by Mathematica. We add the line , for fixing the parameter .

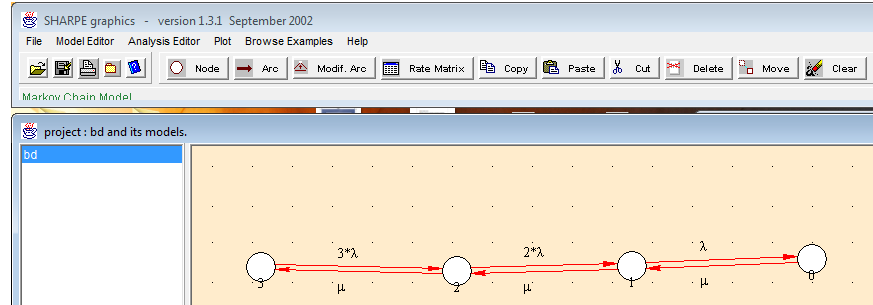
Even fixing some parameters, sometimes the Markov Chain is too complicated to obtaining closed formulas. We can fixing all parameters for obtain exact steady state probabilities for all states (instead closed formulas), but we also have a option for convert the IDES diagram in a SHARPE project to perform some calculations performed by this software. Figure 5 shows the created SHARPE project for the birth-death model of the example. We created this project by invoking the following command:

java -jar IDESParser.jar --sharpe bdprj bd model

, that produces those two files: bd.rgl (project file) and bd_model.mkv (Markov model file).

Click HERE to download.

Bibliography

1

Rudie, Karen. “The integrated discrete-event systems tool.” Discrete Event Systems, 2006 8th International Workshop on. IEEE, 2006.

2

Sahner, Robin A., and Kishor S. Trivedi. “Reliability modeling using SHARPE.” Reliability, IEEE Transactions on 36.2 (1987): 186-193.

3

Wolfram, Stephen. The MATHEMATICA® Book, Version 4. Cambridge university press, 1999.

4

Bjarne E. Helvik. Statediagrams.m; a Mathematica package for dependability analysis of systems by CTMC. Unpublished NTNU, 2002. Available athttp://library.wolfram.com/infocenter/MathSource/7370/